√1000以上 直角 三角形 角度 の 求め 方 223082-直角三角形 角度の求め方 2辺

証明の書き方合同な三角形の証明問題の書き方を基礎から解説！ 直角三角形証明問題の書き方とは？合同条件の使い方を徹底解説！ 二等辺三角形の角度の求め方 厳選6問解説！←今回の記事 正三角形の角度 正方形、ひし形との融合問題を解説！从已知两边求角度 若我们知道 直角三角形 两条边的长度，我们便可以求三角形的未知角度。 例子 梯子搁在墙上，如图。 梯子与墙之间的 角度 是多少？2 三角形の外角 21 三角形の1つの外角は、その隣にない2つの内角の和と等しい;

1

直角三角形 角度の求め方 2辺

直角三角形 角度の求め方 2辺-直角三角形の角度の出し方を教えてください！！ 直角三角形で、3辺の長さがわかっている場合に残り2つの角度の出し方を教えてください！！①電卓がある場合（関数機能のないもの。ルート機能だけある Read 523 直角三角形の角度の求め方 教えて下さい。鈍角の三角比の例題 90°を超える三角比1（1°） 90°を超える三角比2（135°、150°） 180°－θの三角比 三角比からの角度の求め方1（sinθ） 三角比からの角度の求め方2（cosθ） 三角比からの角度の求め方3（tanθ） 鈍角を含む三角比の相互関係1（図の利用

三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三平方の定理の拡張（中学校の数学との関係） 右図1のような直角三角形については、 a 2 =b 2 c 2 （1） が成り立ちます。（三平方の定理） では、図2のように∠ A が 90 ° でないときには、この定理はどんな形になるのでしょうか。 二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう！ 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な 直角三角形の角度の求め方 こんにちは！ 大神です。 今日は学校の 勉強は大事だよ ということを書いていこうと思います。 突然ですが皆さんは 「直角三角形の角度の求め方」 の公式を覚えていますでしょうか？ サイン・コサイン・タンジェント

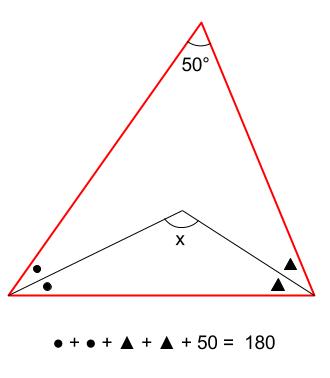
直線の角は180°であることより ㋐＋㋐＋70° ＝180°なので、 ㋐＋㋐ ＝110° ＝55° となります。直角三角形の2辺の情報を元に外周を求める 1 直角三角形を理解する 直角三角形とは、角の1つが直角（90度）になっている状態を意味しています。 その直角の反対側にある辺は常に3辺の中で最も長く、斜辺と呼ばれています。 まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。 例えば、次の直角三角形ABCがあったとして、辺BCの長さが2cmだったとしよう。

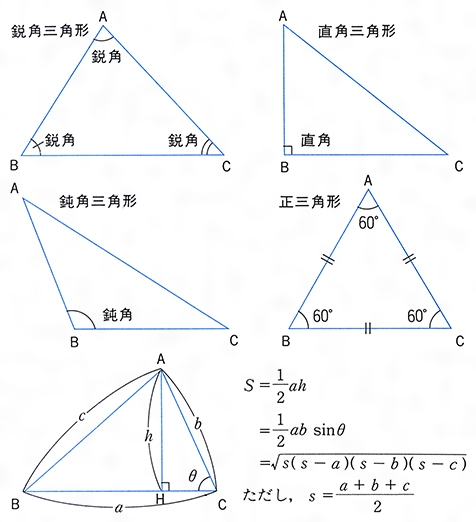
 正三角形の1つの角の大きさが60°で角は3つだから 60×3＝180だね。 三角定規はどうだったかな。 角のせいしつ 三角定規 検索 三角定規（直角二等辺三角形）：45°・45°・90° 三角定規（直角三角形）：30°・60°・90° 三角形の内側の角の大きさの合計の事を「内角の和」といい、全ての三角形は180°です。 三角形の内角の和が180°はわっかったけど、外角の定理って q 直角三角形の斜辺の長さの求め方（三角関数） 直角三角形の直角を挟む2辺の長さが与えられている場合。 例えば、30と15の場合、残りの小さい方の角度はatan(15/30)で約26度と求まる事までは思い出しました。S formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC = 180 T r i a n g l e u s i n g H e r o n ′ s f o r m u l a ( 1) S = s ( s − a) ( s − b) ( s − c), s = ( a b c) 2 ( 2) i f a ≥ b, c h = 2 S a, B

角度の求め方 角度の求め方 Mqttk

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

直角三角形の高 直角三角形の高さを求めるための式 さを求めたい 「＝11＊SIN（RADIANS （36））」と入力 三角関数とは逆に「辺の長さから角度を求める」には、逆三角関数を使い ます。逆三角関数にはアークサイン（arcsin、逆正弦）、アークコサイン二等辺三角形の角度の求め方（計算） 色々な二等辺三角形の角度を求めましょう。下図をみてください。頂角が90度です。前述した計算式を使います。 α2θ＝180 902θ＝180 2θ＝90 θ＝45 頂角が直角の二等辺三角形を、直角二等辺三角形といいます。次の問題です。ここで，定義をもう一度確認しておきましょう。 このように，定義は式だけでなく条件まで正しく覚えて使えるようにしておきましょう。 では，例題のような「直角三角形ではない三角形」で，3辺の長さが与えられたときはどのように解くのでしょうか。 この問題では，3辺がわかっていて1つの角の余弦の値 (cos B の値)を求めるので， この問題のように

配管作業で使える角度絡みの計算方法 配管継手寸法表のまとめ

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

 Contents 1 三角形の内角 11 問題; 直角三角形の角度tanθの求め方 底辺 1800mm 高さ 3mm の直角三角形のtanθ ベストアンサー：三角形のイメージを明確にするために、直角三角形の一番長い辺を上にして、 直角を右にくるようにしたとき水平となった辺を底辺と呼び、その長さを1800mm、 垂直な辺を高・直角三角形(斜辺と角度) 直角三角形の斜辺と角度から、底辺と高さと面積を計算します。 三角関数 ・ 角度から三角関数 角度(度またはラジアン)から三角関数を計算します。

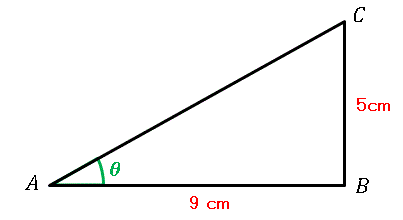
Excel で直角三角形の斜辺と底辺に挟まれた角度を求めます

中２数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン

計算すると、 4 9 = c × c 13 = c × c よって、長い辺の長さは c = 13 （二乗して 13 になる正の数）となります。 では、 13 はどれくらいの長さでしょうか？ 3 × 3 = 9 c × c = 13 4 × 4 = 16 なので、 13 は 3 より大きくて 4 より小さい数だと分かります。Right triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos ⁡ θ = a c , sin ⁡ θ = b c , tan ⁡ θ = b a ( 2) P y t h a g o r e a n t h e o r e m a 2 b 2 = c 2 お客様の声3 三角形の種類（鋭角、直角、鈍角） 31 何三角形？ 見極め方ポイント

三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題

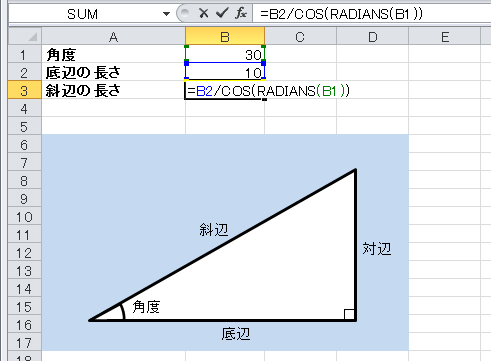
角度からコサインを計算するには Cos Radiansの解説 エクセル関数リファレンス

左側の直角三角形から角度を求めると、 θ＝180°－30°＝150° だね。 答え 三角比からの角度の求め方1（sinθ） タレスの定理（直径に対する円周角は直角）から \(∠abd=90°\) \(at\) は円の接線⇔ \(∠tad=90°\)（後述） より、\(∠bat=90°∠bad\) 三角形の内角の和は \(180°\) より 下の四角形のaの角度を求めなさい。 解説 下の図のように四角形の1本の対角線で2つの三角形に分けます。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2＝360°になります。 中学受験をする子供の読書習慣の身につけ方合格する子が

三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

重なり合う三角定規を使った角度の計算問題 小4 小５の算数 きいとこ

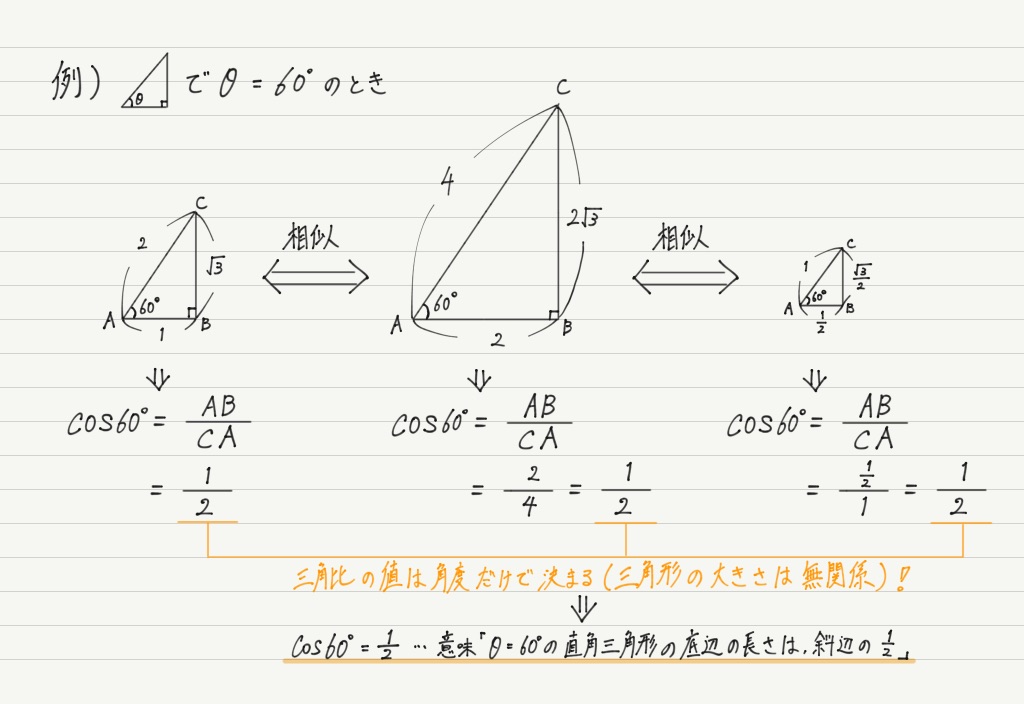
それでは実際に直角三角形の解法をしてみましょう。ここでは、具体的に次のような直角三角形を考え、分かっていない残りのB, a, bを求めたいと思います。 角Bの値 まずは、角度Bは簡単に求まります。 三角形の内角の和は180度ですから、「C = 180 A B = 180 35 90 = 55」より、角Cの大きさは55度だと分かります。 aとbの求め方 次に、aとbを求めてみましょう。 三角解説 三角比というのは，与えられた角度に対して，ただ1つ値が決まるもので，その角度が「どんな形の三角形の角の大きさであるか」にはよらないからです。 この話を考えるとき，三角比の 「値を求める」 のか， 「値を利用する」 のかを区別して考えてみましょう。

タンジェントとは何か 中学生でも分かる三角関数の基礎

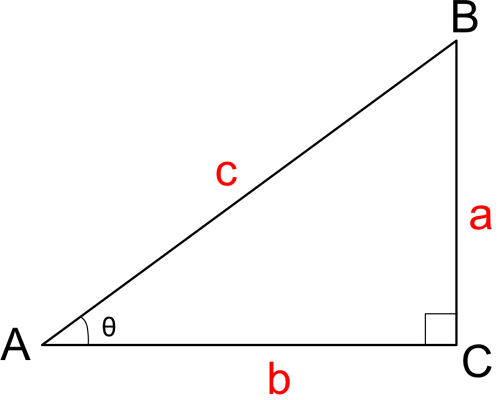
上級 三角関数 Shade3d チュートリアル

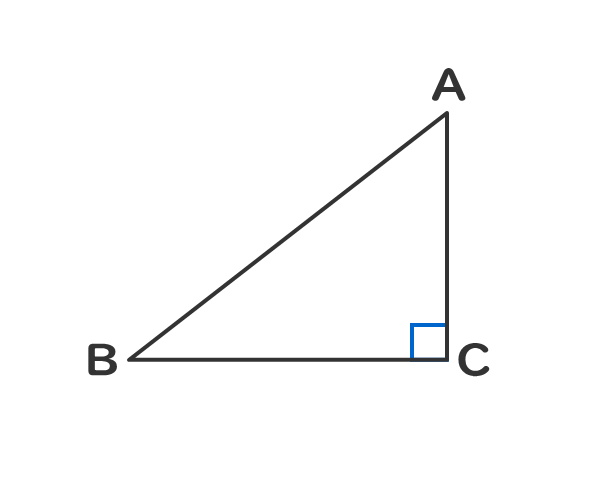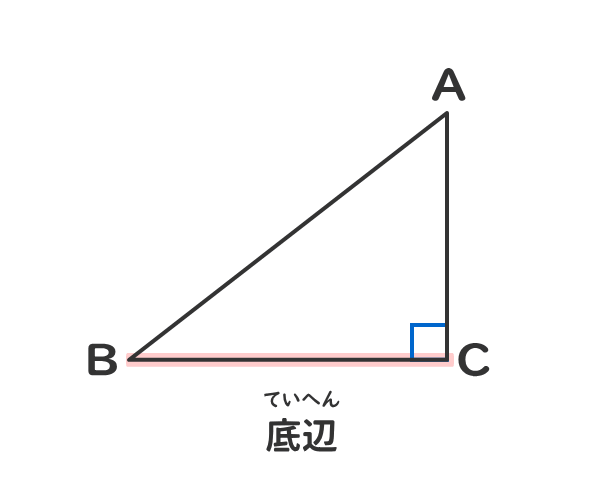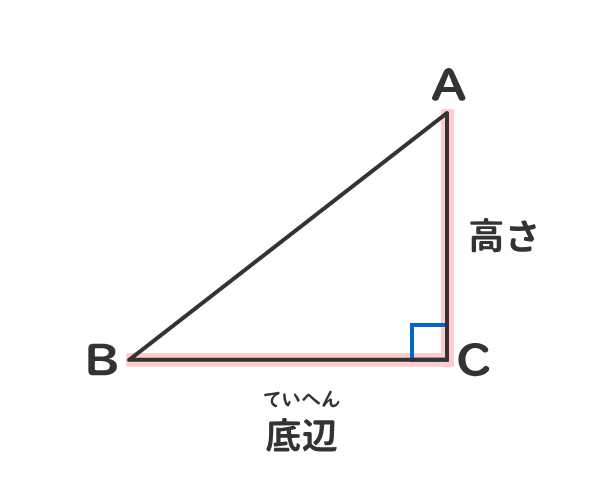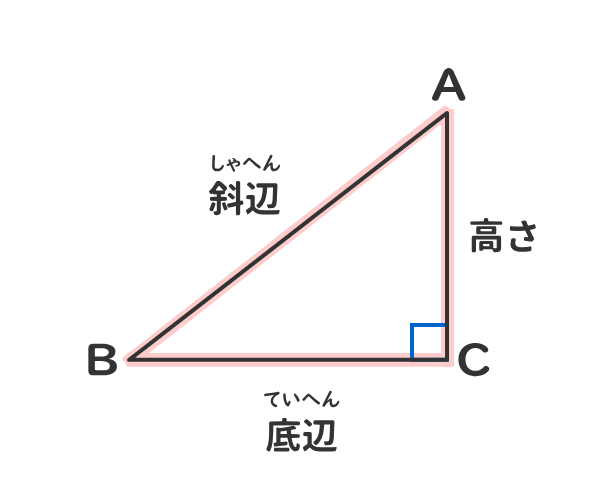
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web

直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo

二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典

三角形の角度を求める問題 小学生 中学生の勉強

直角三角形の解法 1

タンジェントとは何か 中学生でも分かる三角関数の基礎

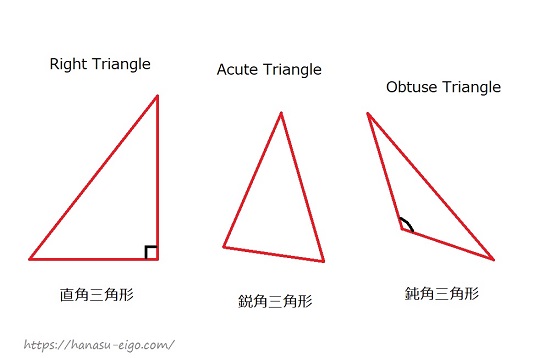
三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語

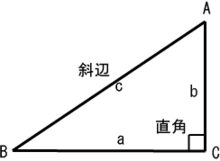
直角三角形 Wikipedia

直角三角形の解法 1

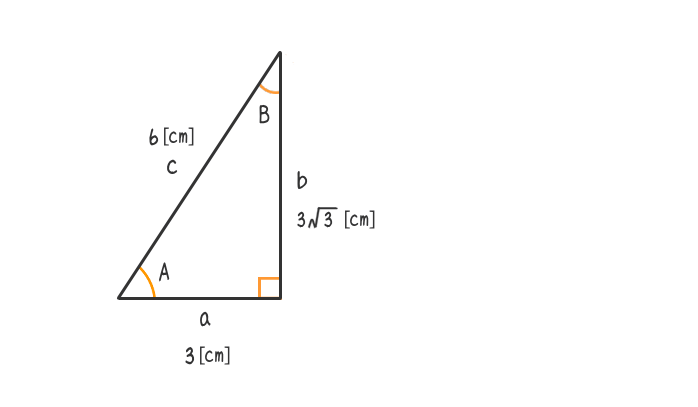
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web

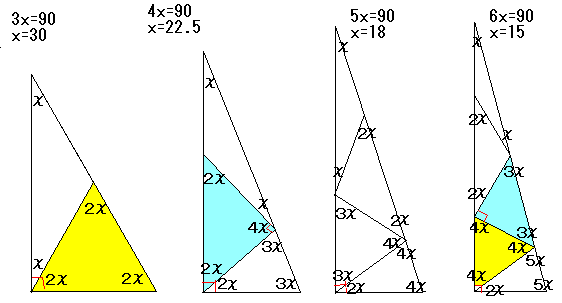
はしご直角三角形

三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ

1

斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める

直角三角形の角度の求め方 教えて下さい 斜辺以外の２辺の長さが分かっ Yahoo 知恵袋

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

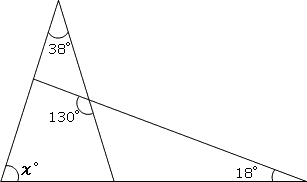
角度の求め方 算数の教え上手 学びの場 Com

三角形の３辺から角度を計算 高精度計算サイト

二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web

直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora

小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

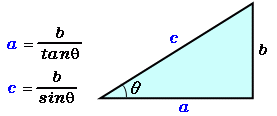
角度と高さから底辺と斜辺を計算 高精度計算サイト

直角三角形の角度と辺の長さの求め方を教えて下さい Okwave

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

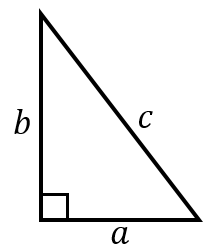
直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学

Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算

15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext

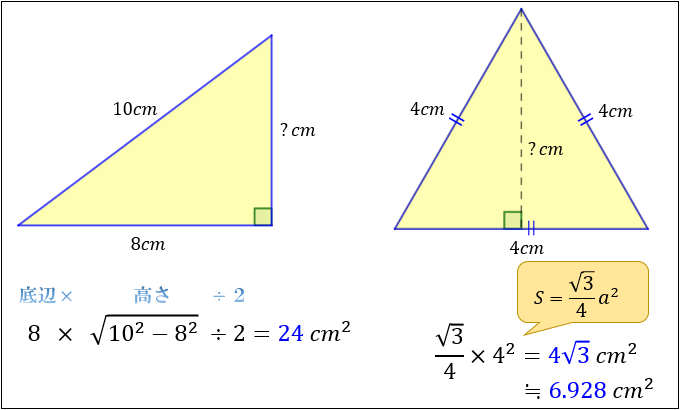
三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

1

小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ

直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

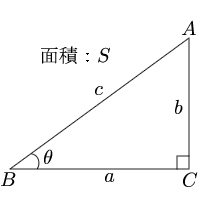
直角三角形 底辺と角度 三角形の計算 計算サイト

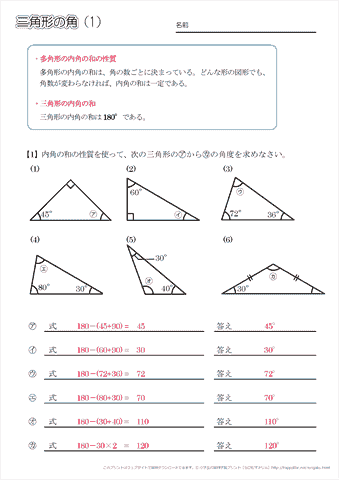
小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

直角三角形の底辺と高さで角度を求める 電卓で墨だし計算 Teacup ブログ Autopage

二等辺三角形の角を求める Youtube

Javaでmathクラスを使って三角関数を求める方法を現役エンジニアが解説 初心者向け Techacademyマガジン

簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく

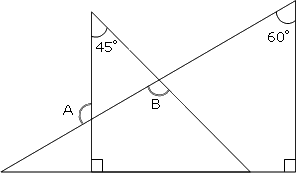
角度の求め方 算数の教え上手 学びの場 Com

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

1

底辺と高さから角度と斜辺を計算 高精度計算サイト

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

底辺と角度から 高さを求める ある高さの木から 10m離れて 木の 数学 教えて Goo

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

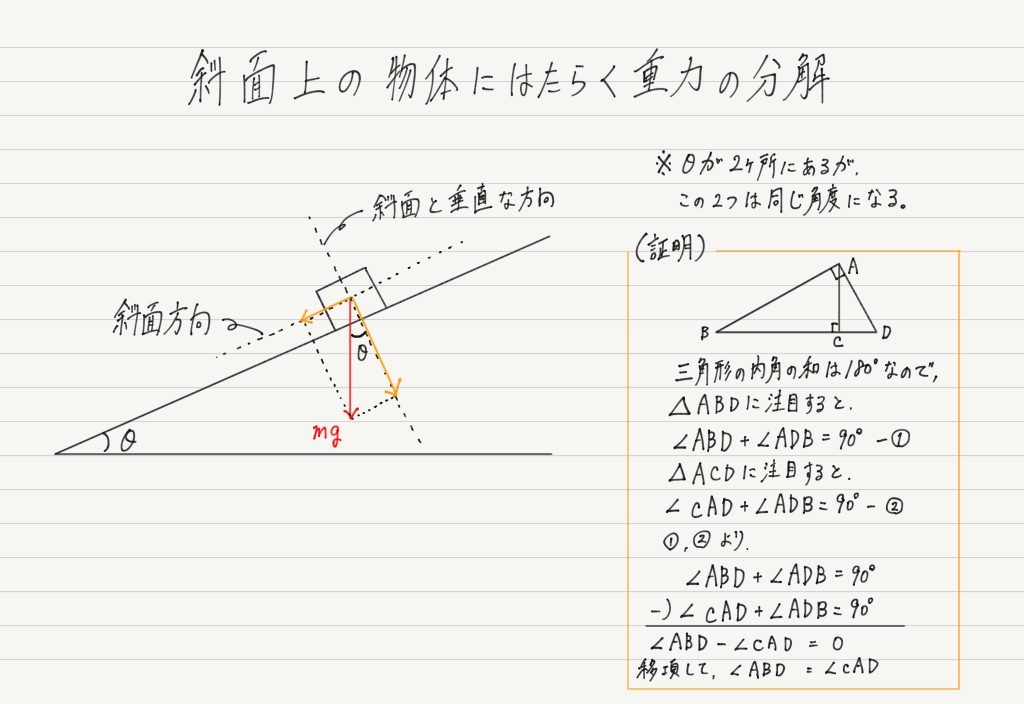
力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に

3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ

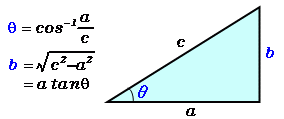
底辺と斜辺から角度と高さを計算 高精度計算サイト

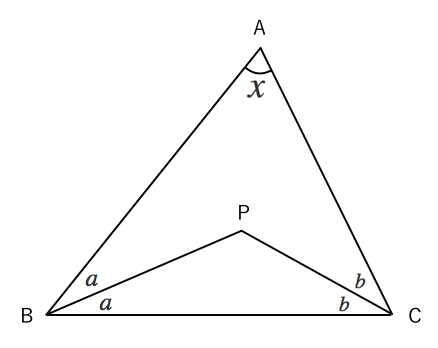
図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に

二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

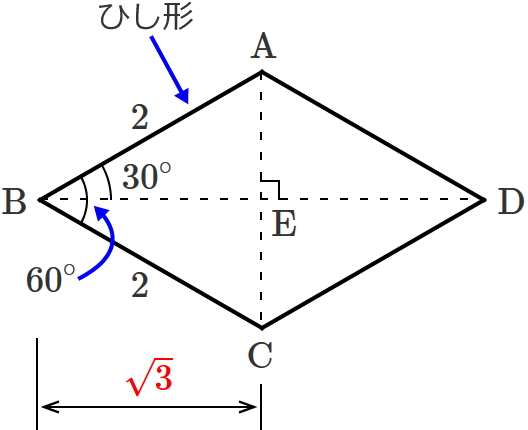
ひし形の対角線の長さの求め方

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める

直角三角形の高さは 1分でわかる計算 求め方 公式 直角二等辺三角形の辺の長さ

Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ

中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ

高校数学 三角形の辺と角の関係 映像授業のtry It トライイット

小５ 算数 小５ ３１ 三角形の角 Youtube

三角形とは コトバンク

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

直角三角形の辺を求める Youtube

三角形の角度を求める問題 小学生 中学生の勉強

三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に

1

中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su

正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

三角形の辺から角度を計算 製品設計知識

普通の電卓で計算できる直角三角形の近似計算

直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

高校数学 三角比からの角度の求め方2 Cos8 例題編 映像授業のtry It トライイット

直角三角形の斜辺の長さと角度が分かっている場合 他の2辺の長さを求めたいので Yahoo 知恵袋

交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー

正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

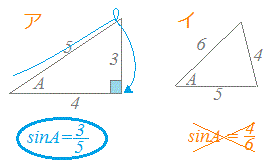
正弦定理

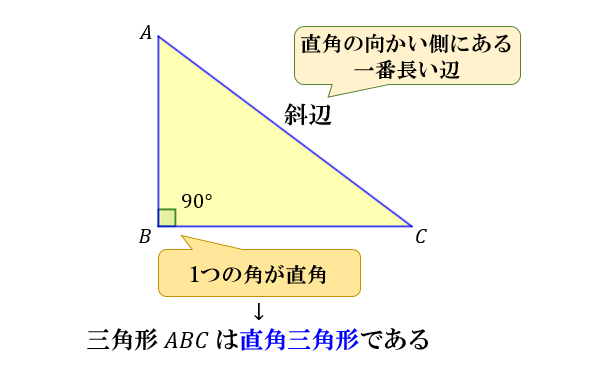
直角三角形の辺の長さ 合同条件 面積について アタリマエ

三角関数をマスターしよう その2 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す

直角三角形の底辺の長さは 1分でわかる計算 斜辺 高さ 角度との関係

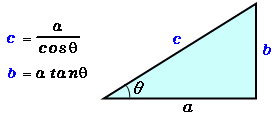
角度と底辺から斜辺と高さを計算 高精度計算サイト

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

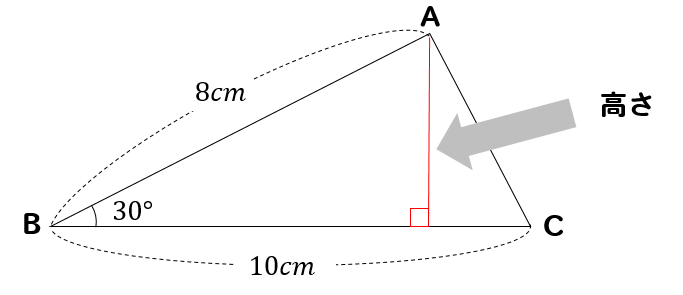
小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ

1 1 ルート2 三角形

簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三角比について

Incoming Term: 直角三角形 角度の求め方, 直角三角形 角度の求め方 電卓, 直角三角形 角度の求め方 2辺,